The School of Physics has a long history of excellence in the field of mathematical physics beginning in the early 1970s with the pioneering work of Emeritus Professor R J Baxter. The current interests of the mathematical physics group, which spans the Department of Fundamental and Theoretical Physics and the Mathematical Sciences Institute, are primarily in the fields of exactly solved models in statistical mechanics and quantum field theory and in mathematical aspects of string theory and conformal field theory. The research goals of the group involve building on its unique legacy to further develop fundamental research in these areas.
The study of exactly solved (integrable) lattice models in statistical mechanics is an area in which Australia has a leading international reputation. The knowledge and understanding obtained from exactly solved models has greatly enhanced progress in the theory of phase transitions and critical phenomena.

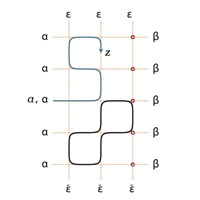
Recently it was discovered that fundamental algebraic structures of the theory of integrable systems, such as Yang-Baxter equations and quantum groups, are connected to quantization of elementary incidence theorems in three-dimensional geometry. A key role in this setting is played by circular nets in 3D (like the one shown on the picture) which provides remarkable examples of discrete Hamiltonian evolution systems.

Condensed matter physics has a goal of understanding the structure and properties of all kinds of solids and liquids. It is a very broad and lively area of research, where one witnesses frequent occurrence of novel phenomena relating to exotic properties of matter in semiconductors, superconductors, magnets etc. Due to intense research all over the world in this area, new ideas and novel materials are created. Needless to say, today condensed matter physics is one of the main pillars of high technology.
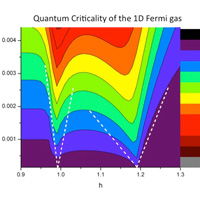
Over the past ten years remarkable experimental achievements have exposed the great beauty and subtlety of physics near absolute zero. For example, the nature of bosons, which can occupy the same quantum state, and fermions, which cannot occupy the same quantum state, are observable in experiments with ultracold Bose and Fermi gases. Integrable (exactly solved) models play a crucial role in the study of quantum effects in low-dimensional many-body systems of this kind.

Lattice integrable systems have led to a remarkable progress in many research areas of physics and mathematics including quantum groups, topology, combinatorics, 2D conformal field theory and condensed matter physics. This project aims to study recently discovered connections between mathematics of 2D integrable systems on finite lattices, the combinatorial 3-coloring problems on square grids and the theory of special functions.

Application and development of variational algorithms and the corner transfer renormalization group. The numerical corner-transfer matrices (CTM) method is a powerful variational algorithm suitable for studying 2D and 3D systems in statistical mechanics and quantum physics. With some modifications it can be also used for investigating properties of 1D and 2D quantum systems.