Exactly solved models in cold atoms and spin systems

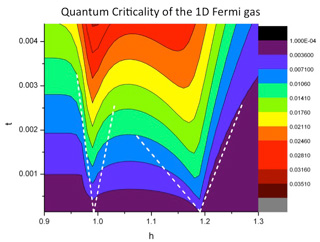
Over the past ten years remarkable experimental achievements have exposed the great beauty and subtlety of physics near absolute zero. For example, the nature of bosons, which can occupy the same quantum state, and fermions, which cannot occupy the same quantum state, are observable in experiments with ultracold Bose and Fermi gases. Integrable (exactly solved) models play a crucial role in the study of quantum effects in low-dimensional many-body systems of this kind.

In particular, recent breakthrough experiments on trapped ultracold bosonic and fermonic atoms confined to one dimension have provided abetter understanding of quantum correlations and quantum critical phenomena predicted from exactly solved many-body systems. Typical exactly solved systems in the more traditional setting of condensed-matter physics are quantum spin chains and ladders, strongly correlated electron systems, the Hubbard model, and the Bardeen-Cooper-Schrieffer pairing model.

We have made a number of contributions to the study of these fundamental models, which have led to direct applications in the key recent experiments. This includes work on the two-component Fermi gas and the super Tonks-Girardeau gas, both of which have been realised in experiments [see the articles in Nature 467 (2010) 567 and Science 325 (2009) 1224].

Our current work is on exploring the physics of these and other fundamental mathematical models which are applicable to future experiments.

Contact

Xi-Wen Guan

(02) 612 52968