» Research » Department of Quantum Science and Technology » Laser physics, optics and photonics group » Complex beams, optical guides and laser trappingIt has been almost thirty years since the so-called non-diffracting propagation of electromagnetic waves was proposed. The beams that show this behaviour are formed by the interference of plane waves, with wave vectors covering a conical surface. Some of the characteristic features of this effect are the division of the total power of the beam in several concentric rings, restricting the reachable maximum at the central ring, and the shrinkage of the central beam core, focusing this limited power in a tiny area and thus obtaining a substantial intensity increment. The simplest of these non-diffractive beams is called Bessel beam of zero-order because its radial profile can be described by the Bessel function of the first kind and zero-order, producing a beam with a bright central core and a limited number of concentric rings surrounding it. However, more complex Bessel beams can be build using high-order Laguerre-Gaussian (LG) beam field distributions as a base for the interference effect. These high-order LG beams have a doughnut shape on its radial profile, which consequently will create non-diffracting beam that has a similar radial profile, now with a central ring surrounding a dark core.
Our research program is divided into three streams:
Non-diffracting optical quasi-Bessel beams provide an opportunity to construct optical fields of complex architecture. The constructed beams may have a bright central peak or zero intensity on the beam axis and have the beam size of only a few microns propagating over a long-defined distance, which is not possible with conventional Gaussian or high-order Laguerre- Gaussian beams.
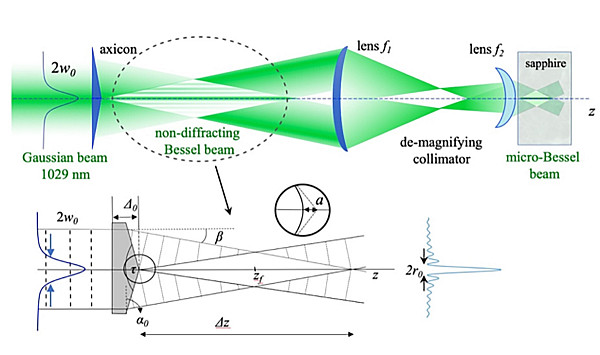
Formation of a Bessel beam from a Gaussian beam with waist w0 by an axicon with a wedge angle ⍺0 and re-imaging it into transparent media using a two-lens de-magnifying collimator.
During the last decades, it was demonstrated that ultra-short intense laser pulse tightly focused deep inside a transparent dielectric generates energy densities in excess of several MJ/cm3. Such energy concentration with extremely high heating and quenching rates leads to unusual solid-plasma-solid transformation paths overcoming kinetic barriers for the formation of previously unknown high-pressure material phases. There are two limitations however on the energy density and amount of laser-affected material in confined micro-explosion generated by tightly focused Gaussian beam. First is imposed by the laser pulse diffraction, limiting the radius of the focal spot. Combined with the absorption depth of the laser pulse energy in plasma formed, which constitutes 30-60 nm in solid density plasma, the sub-micron size volume of the laser affected material is rather small, less than a nanogram. This constitutes the second limitation, which is the number of laser-affected atoms of only around 1010 – 1012 atoms in a single laser shot. While the absorbed energy density is in the order of 107 J/cm3, resulting in ~10 TPa achievable pressure, the small volume of the new atomic arrangements makes structural studies extremely complicated.
It was demonstrated recently that the Bessel-shaped pulse transforms a much larger amount of material in a single pulse. Due to cylindrical geometry of the shock wave expansion it allegedly creates higher energy density than that previously achieved. It was also demonstrated as an efficient tool for fast material processing. Thus, diffraction free Bessel-like beams promise to achieve significant increase the amount new material structures produced by the micro-explosion technique.
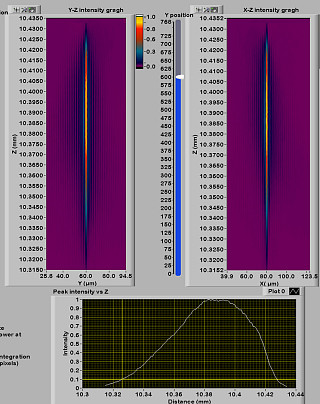
Shown above right is the measured 1030 nm wavelength Bessel beam with a <1 micron diameter central core produced by the axicon which meets the diffraction limited theoretical performance.
Constructing a needle-like diverging optical funnel with zero intensity on the axis: The primary aim is to numerically construct and optimize the optical field, which could transversely compress and focus a stream of µm- and sub-µm size particles injected into vacuum or gaseous environment by applying light pressure and photophoretic forces pushing particles into the area with lower intensity. We modelled numerically an optical funnel based on re-imaging a non-zero-order quasi-Bessel beam, formed by an axicon and a phase plate or using an SLM, with a collimator. The funnel geometry, namely, the μm-size of the beam cross-section, several-mm long propagation length and its divergence, is controlled and optimized by changing the topological charge at a fixed collimation of the re-imaging optics, or/and by varying the collimation with fixed topological charge of the beam.
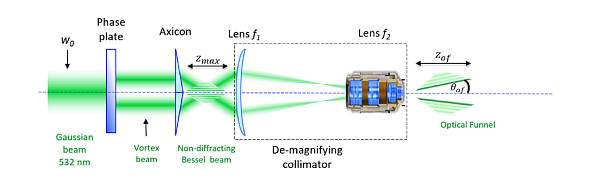
Construction of optical funnels using a phase plate and an axicon. This combination of the optical elements shapes the phase distribution of the incoming beam, creating a non-diffracting quasi-Bessel beam. After that, it is re-imaged with a de-magnifying collimator, thus building a slow-diverging Bessel-Gaussian beam, an optical funnel.
Simulated profiles have an application for optical guiding and focusing of aerosolised beam of particles, large biomolecules and viruses to the micron-size focus of x-ray Free Electron Lasers in order to increase the delivery efficiency of isolated single particles in coherent diffractive imaging experiments.
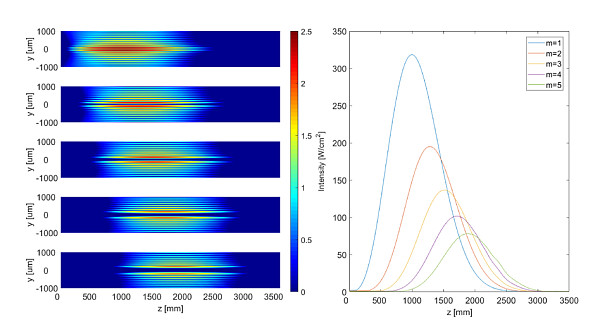
(Left) Simulated axial propagation of Bessel beams with topological charge from 1 to 5 and an axicon angle equal to 0.3 degrees. The intensities have been denoted in logarithmic scale. As predicted, their lengths do not change notoriously, but its propagation positions are extended over the axial direction, depending on m. (Right) Intensity distribution comparison over the axial propagation. It can be noticed that the maximum intensity is about 350 W/cm2 (with the input beam power of 1 W) for the first-order Bessel beam, and it decreases along the increasing of m, consequence of the hollow core expansion.
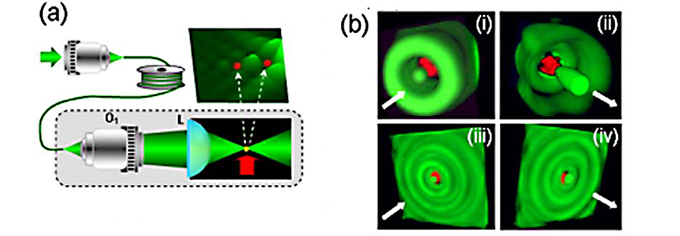
We recently introduced a new technique of trapping nanoparticles in air using optical vortices. The technique is based upon thermal forces induced by uneven heating of light absorbing particles with a laser beam. The laser vortices with doughnut-shaped intensity profile provide a means to trap particles and push them along the zero-intensity beam axis to a desirable location. Our studies cover optical trapping, guiding, and pin-point positioning of particles in air, as well as simultaneous trapping thousands of particle with a single laser beam. Optical vortices can be applied to touch-free transport of containers holding gases, ultra-pure or dangerous substances, and biological macromolecules.
Laser trapping and agglomerating nanoparticles can be applied for monitoring and removal of nano-pollutants from air, offering a new avenue toward environmental protection in the workplace of the nanotechnology industry. We apply this approach to photophoretic traps in air, and investigate the dependence of trap stiffness on laser power, polarization state, and gas pressure.
We analyse the equilibrium positions of trapped spheres depending on laser power and polarisation. This effect, brought about by the balancing of weight and trapping force, could in principle be used to weigh single particles with masses ranging from picograms to 100s of nanograms. Analysis of a particle's motion can recover information about the particle, the trapping forces and the medium in which the particle is trapped.
Menu
Search 
