There are two major areas of research being pursued by the Applied Topology and Geometry group: topological data analysis (TDA) and topological crystallography. The group has close connections to the Department of Materials Physics and the Mathematical Sciences Institute and frequently co-supervises honours and HDR students.
Topological data analysis is a new field that applies the mathematical theory of homology to quantify the number of pieces, tunnels, voids and higher-dimensional cycles in a space approximated by finite data. The TDA community has developed robust and efficient software for computing these quantities from point-cloud and digital image data. The group at ANU is at the forefront of these developments and explores their application to micro-CT images of porous and granular materials, self-assembly of particles interacting under pair-potentials, and many other areas.
Mathematical crystallography develops connections between geometry, topology and group theory to enable the study of periodic structures. The group produced and maintains the EPINET database of periodic nets and has ties to RCSR: the Reticular Chemistry Structure Resource. These databases provide a rich source of models for scientists and engineers to test theories against.
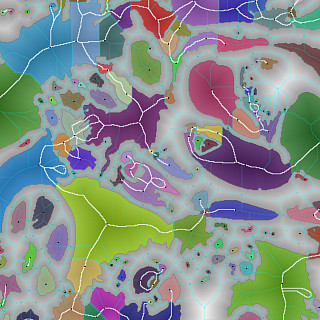
The properties of materials are governed by their structure, for example the size and arrangement of pores, grains and cells. We study the mathematics of these parameters – topology - and compare with advanced three-dimensional x-ray imaging, which can now reveal the internal detail of micro-structured materials, enabling investigation of the relationship between microstructure and physical properties.

This is a long-term project with Stephen Hyde and Stuart Ramsden to construct three-dimensional crystalline structures via two-dimensional hyperbolic geometry. Our investigations of theoretical structures have led to new models for materials including metal-organic frameworks, light-weight rigid isotropic microstructures, and insights into the way keratin filaments are arranged in mammalian skin.